{
“MyObject”: [
{
“title”: “國中童軍學習單-上冊”,
“subtitle”: “”,
“img”: “https://website.hle.com.tw/mgz/image/jco/國中童軍學習單-綜合(上).jpg”,
“year”: “114學年度 上學期”,
“category”: “學習單本”,
“description”: “國中綜合活動童軍學習單,教師教學亦可搭配7-9上共用。”,
“categoryid”: “”,
“link”: [
{
“name”: “國中童軍學習單-綜合(上)”,
“file”: “https://website.hle.com.tw/mgz/file/jco/國中童軍學習單-綜合(上).pdf”
}
]
}
]
}
作者:教學科-組別1
國中輔導學習單-上冊
{
“MyObject”: [
{
“title”: “國中輔導學習單-上冊”,
“subtitle”: “”,
“img”: “https://website.hle.com.tw/mgz/image/jco/國中輔導學習單-綜合(上).jpg”,
“year”: “114學年度 上學期”,
“category”: “學習單本”,
“description”: “國中綜合活動輔導學習單,教師教學亦可搭配7-9上共用。”,
“categoryid”: “”,
“link”: [
{
“name”: “國中輔導學習單-綜合(上)”,
“file”: “https://website.hle.com.tw/mgz/file/jco/國中輔導學習單-綜合(上).pdf”
}
]
}
]
}
國中家政學習單-上冊
{
“MyObject”: [
{
“title”: “國中家政學習單-上冊”,
“subtitle”: “”,
“img”: “https://website.hle.com.tw/mgz/image/jco/國中家政學習單-綜合(上).jpg”,
“year”: “114學年度 上學期”,
“category”: “學習單本”,
“description”: “國中綜合活動家政學習單,教師教學亦可搭配7-9上共用。”,
“categoryid”: “”,
“link”: [
{
“name”: “國中家政學習單-上冊”,
“file”: “https://website.hle.com.tw/mgz/file/jco/國中家政學習單-綜合(上).pdf”
}
]
}
]
}
英語旅讀世界
{
“MyObject”: [
{
“title”: “英語旅讀世界”,
“subtitle”: “TOPIC世界兩大熱氣球嘉年華”,
“img”: “https://website.hle.com.tw/mgz/image/jen/114上國中英語-旅讀世界.jpg”,
“year”: “114學年度 上學期”,
“category”: “主題閱讀”,
“description”: “Explore the World Through Words.透過 8 篇精彩文章,帶孩子走進世界的生活、節慶、科技與流行音樂。另有 114 英語科會考分析,掌握最新教學趨勢!”,
“categoryid”: “”,
“link”: [
{
“name”: “教用”,
“file”: “https://website.hle.com.tw/mgz/file/jen/114上國中英語-旅讀世界(教)合.pdf”
},
{
“name”: “學用”,
“file”: “https://website.hle.com.tw/mgz/file/jen/114上國中英語-旅讀世界(學)合.pdf”
}
]
}
]
}
0915 Taylor Swift Is Getting Married!
{
“MyObject”: [
{
“title”: “0915 Taylor Swift Is Getting Married!”,
“subtitle”: “泰勒絲要結婚了!”,
“img”: “https://website.hle.com.tw/mgz/image/jen/英語時事新聞.jpg”,
“year”: “114學年度 上學期”,
“category”: “”,
“description”: “近期有一則幽默的喜訊:「你的英文老師和體育老師要結婚了。」原來是泰勒絲與美式足球明星特拉維斯.凱爾西宣布訂婚。這則消息讓世界各地的粉絲都興奮不已!”,
“categoryid”: “”,
“link”: [
{
“name”: “基礎版(全文+音檔)”,
“file”: “https://website.hle.com.tw/mgz/file/jen/2025_0915_泰勒絲要結婚了!-基礎版.zip”
},
{
“name”: “進階版(全文+音檔)”,
“file”: “https://website.hle.com.tw/mgz/file/jen/2025_0915_泰勒絲要結婚了!-進階版.zip”
}
]
}
]
}
114生物筆記地圖
{
“MyObject”: [
{
“title”: “114生物筆記地圖”,
“subtitle”: “”,
“img”: “https://website.hle.com.tw/mgz/image/jna/114生物筆記地圖封面.jpg”,
“year”: “114學年度 上學期”,
“category”: “全新學習工具”,
“description”: “筆記地圖幫你把重點拆解成清晰的樹狀圖,再搭配課本圖解概念,快速建立完整架構!藉由提問學習知識點,讓學習不僅止於記憶,而是融會貫通。”,
“categoryid”: “”,
“link”: [
{
“name”: “學用檔案”,
“file”: “https://website.hle.com.tw/mgz/file/jna/114生物筆記地圖學用.pdf”
},
{
“name”: “教用檔案”,
“file”: “https://website.hle.com.tw/mgz/file/jna/114生物筆記地圖教用.pdf”
}
]
}
]
}
翰林因數大挑戰
翰林因數大挑戰
(配合翰林數學課本第24頁)
文/新北市立桃子腳國中小 趙榮華老師
 榮華老師經驗談💭
榮華老師經驗談💭
學生在學習因數時,存有不少學習瓶頸。像是求某一個數的所有因數時,不像加、減、乘、除或四則運算只求一個答案,求因數必須逐一判斷或運算,才能「窮盡」一個數可以被整除的所有情形,稍有遺漏便答案殘缺不完整,進而影響後續的解題過程。為此老師可提供學生補充教材多加練習,以建立學生的「數感」,在求所有因數的問題時,才能又快又完整!
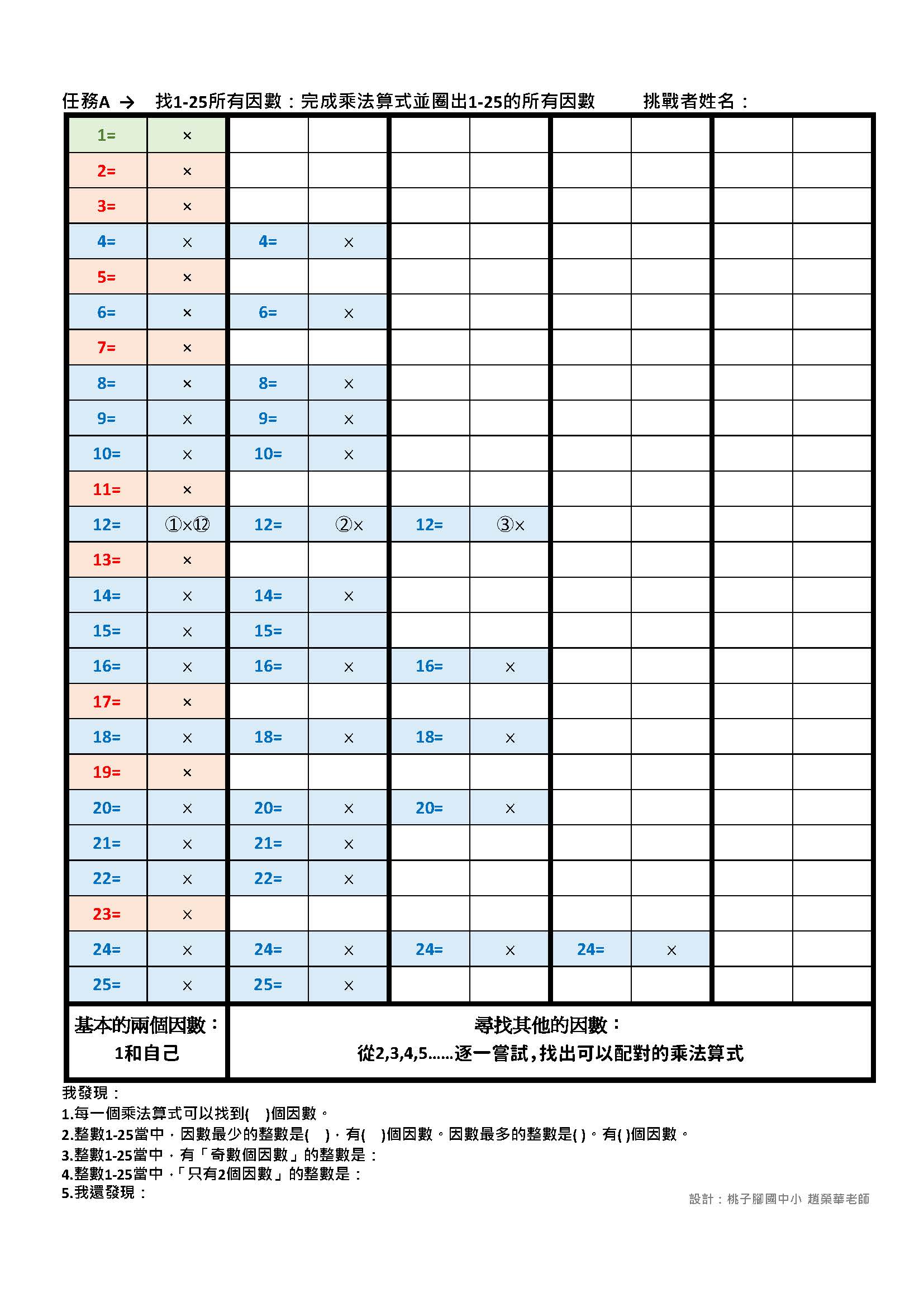
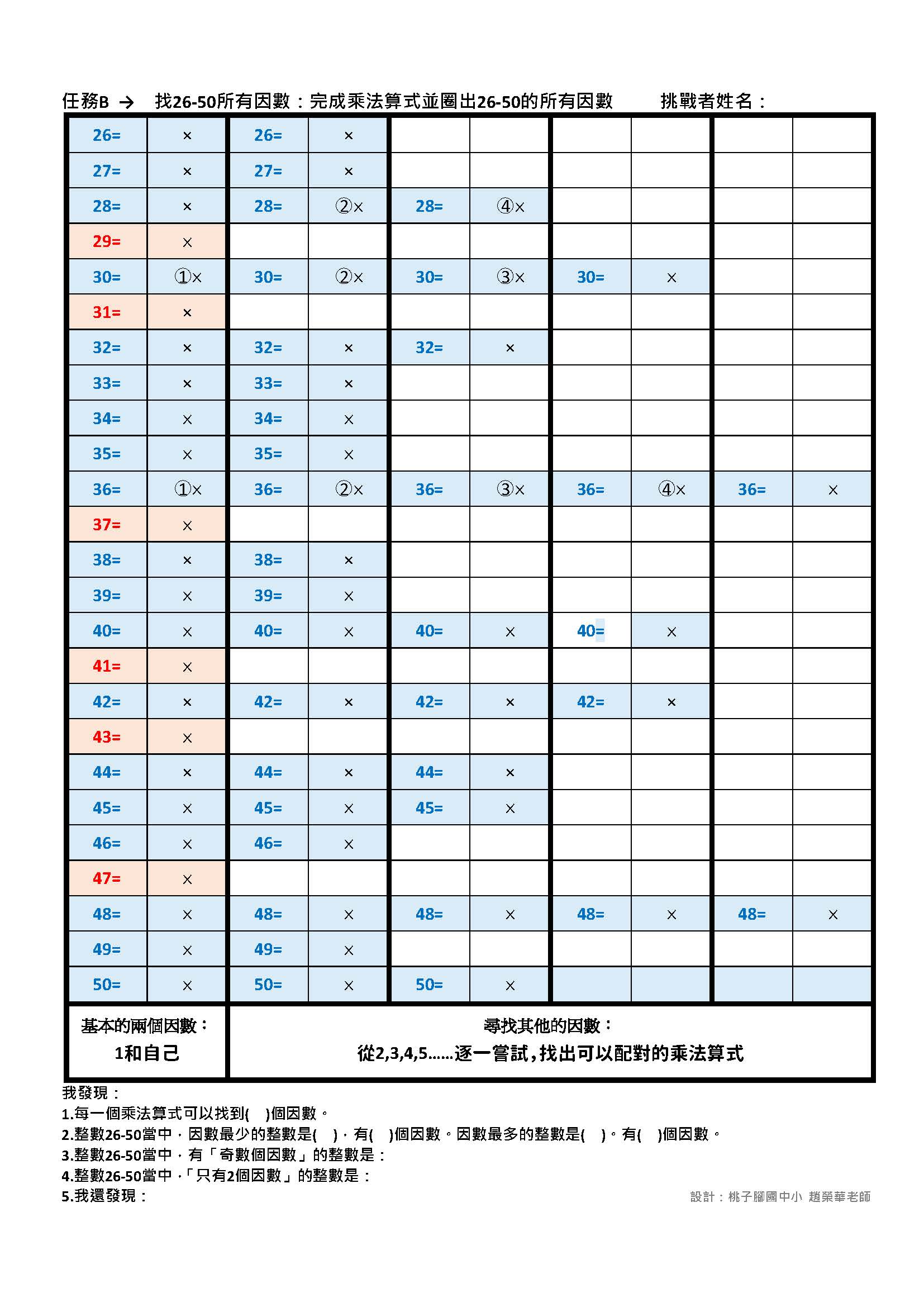
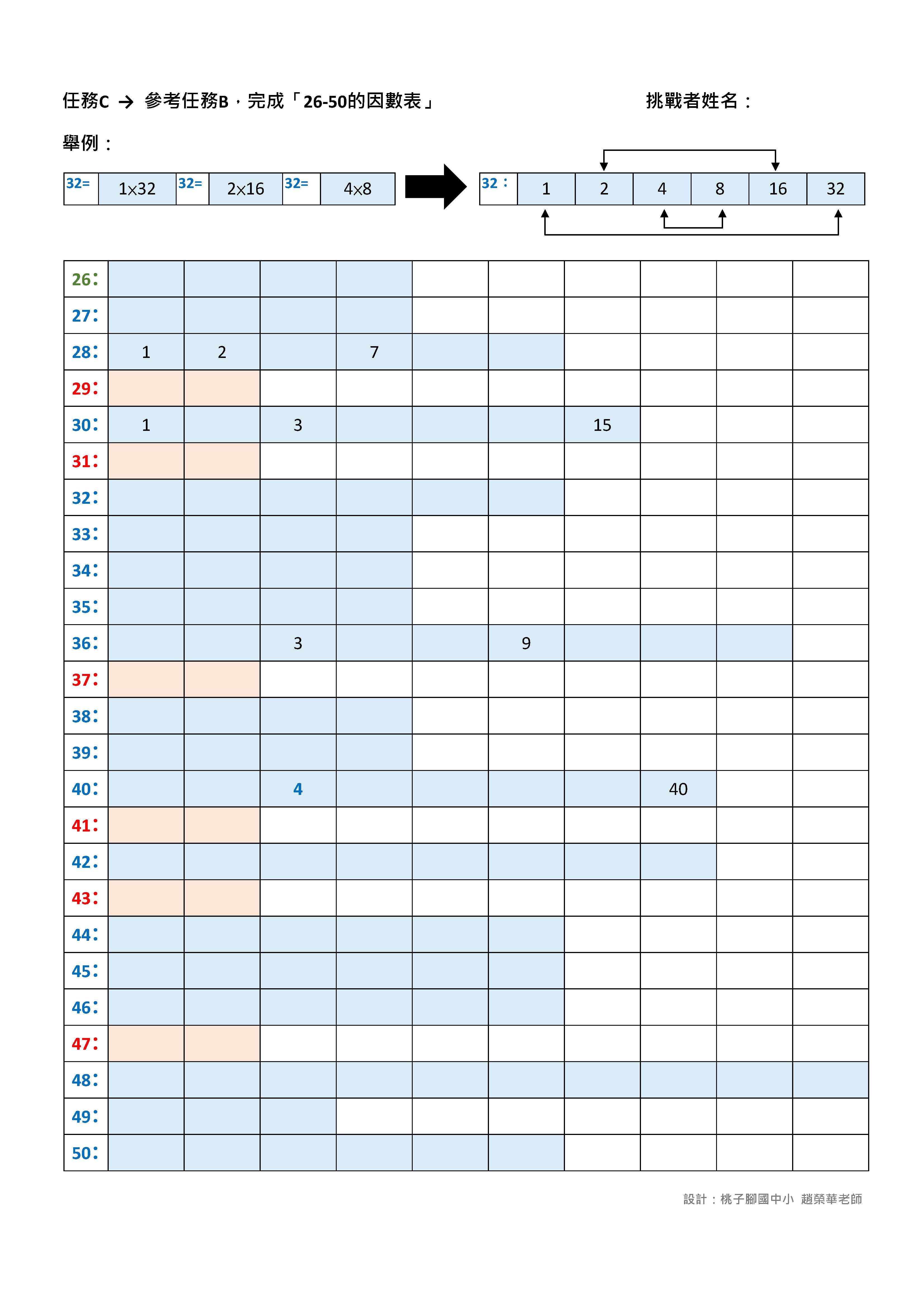
🔹任務A至任務D:利用因數表,認識1-50的所有因數
說明:
1. 先以表格及不同顏色來視覺化呈現整數1-50的所有因數分布情形。只要利用乘法算式,在表格及色塊的引導下,就能逐一求出整數的所有因數。學生在練習之後,能見「樹」亦見「林」,歸納並產生有系統的整理與分類。
2. 如果學習單是以黑白列印,則可提供放大的電子檔,讓學生用綠色、橘色及藍色的色鉛筆來框出色塊範圍,學生自己動手做, 印象會更深刻。
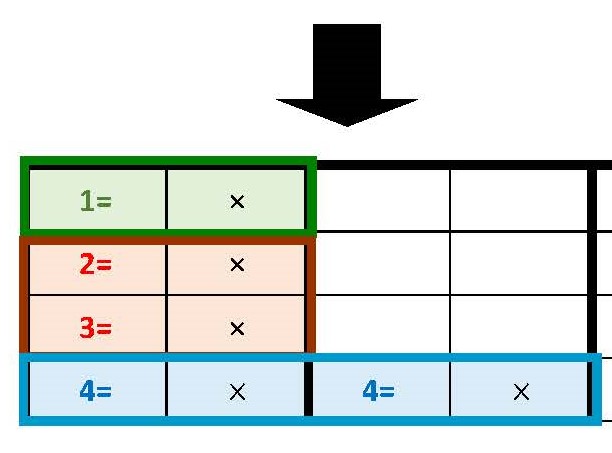
3. 完成的學習單可放置於學習檔案夾,並在接下來的數學課請學生複習內容,教師則反覆抽問任務A及任務B兩
張學習單上的題目。藉由學習單上不同顏色及長度的視覺化呈現,讓學生加深印象並建立數感,在求整數的所有因數時必能駕輕就熟。
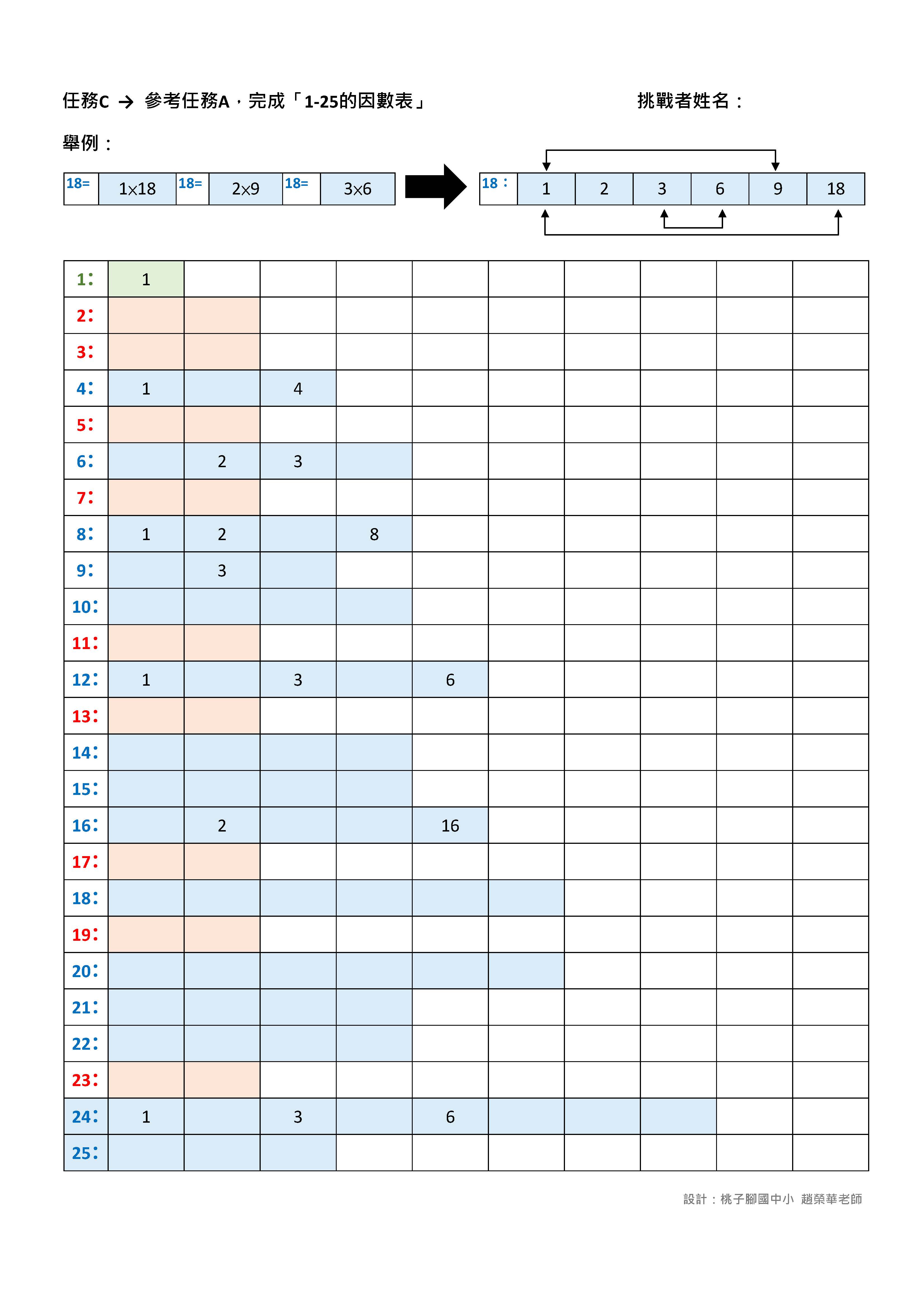
🔹任務E-終極任務: 統整任務A、B、C、D的發現。
說明:
1. 參考整數1-50因數表上的因數個數,將整數分成只有一個因數、兩個因數、四個因數、六個因數、八個因數、十個因數及有奇個因數等,進行分類 。此外,也列出八個因數、十個因數及奇數個因數的整數,加強練習求其所有因數。
2. 學生經任務A、B、C、D的練習之後,比較50以內整數的所有因數個數,歸納整理自己的發現,產生有系統的分類。而有了質數、合數及平方數的基本認知,並輔以重點式的加強練習,在求所有因數的問題時,必能又快又完整!
3. 像這樣讓學生在練習後進行歸納統整的過程,可培養學生主動發現、思考及應用的能力,這在國小高年級的數學課特別重要,也是能否順利銜接國中數學的關鍵之一。
4. 如有時間可如法炮製,讓學生繼續練習求51-100整數的所有因數。

【附件】翰林因數大挑戰學習單 (點我下載PDF)
國小數學-教學互動工具-神祕調查局(錄音室篇)
{
“MyObject”: [
{
“title”: “神祕調查局【錄音室篇】”,
“action”: “1”,
“des”: “統整式遊戲評量,全新課堂互動!結合趣味解謎情境,搭配冊次重點概念,想要順利破關,就先學好數學知識!”,
“icon”: “https://material.hle.com.tw/wp-content/uploads/2025/08/%E7%A5%9E%E7%A5%95%E8%AA%BF%E6%9F%A5%E5%B1%80-6%E4%B8%8A%E9%8C%84%E9%9F%B3%E5%AE%A4%E7%AF%87-%E8%A1%8C%E5%8B%95%E5%A4%A7%E5%B8%AB.png”,
“link”: [
{
“name”: “前往”,
“link”: “https://mystery11.hle.com.tw/”
}
]
}
]
}
國小數學-教學互動工具-神祕調查局(圖書館篇)
{
“MyObject”: [
{
“title”: “神祕調查局【圖書館篇】”,
“action”: “1”,
“des”: “統整式遊戲評量,全新課堂互動!結合趣味解謎情境,搭配冊次重點概念,想要順利破關,就先學好數學知識!”,
“icon”: “https://material.hle.com.tw/wp-content/uploads/2025/08/%E7%A5%9E%E7%A5%95%E8%AA%BF%E6%9F%A5%E5%B1%80-4%E4%B8%8A%E5%9C%96%E6%9B%B8%E9%A4%A8%E7%AF%87-%E8%A1%8C%E5%8B%95%E5%A4%A7%E5%B8%AB.png”,
“link”: [
{
“name”: “前往”,
“link”: “https://mystery7.hle.com.tw/”
}
]
}
]
}
國中社會-歷史年表大事記
{
“MyObject”: [
{
“title”: “歷史年表大事記”,
“action”: “2”,
“des”: “歷史科統整複習神器!一張年表串起臺灣、中國、世界史事件”,
“icon”: “https://h5.hle.com.tw/h5mp4/02j/05So/產品縮圖/歷史年表大事記.png”,
“link”: [
{
“name”: “前往”,
“link”: “https://historytimeline.hle.com.tw/”
},
{
“name”: “網站介紹”,
“link”: “https://youtu.be/I1QK2Hg9W4U”
}
]
}
]
}